 |
>> ОГЛАВЛЕНИЕ
5. Оценка стоимости ценных бумаг предприятия и составление графиков возврата долгосрочных кредитов
5. 1. Оценка стоимости облигаций
Сначала рассмотрим эту задача сначала в классическом варианте для так называемых купонных облигаций. Согласно условиям инвестирования в эти долговые финансовые инструменты предприятие эмитент облигаций обязуется производить периодический процентный платеж на годовой или полугодовой основе и погасить номинальную стоимость облигации к назначенному сроку окончания действия облигаций. Купонная облигация имеют следующие характеристики:
- номинальную стоимость,
- срок до погашения,
- процентную ставку,
- условия выплаты процентов (периодичность выплат).
Сущность оценки стоимости облигации состоит в том, что в течение срока существования облигации ее владелец должен получить ту же сумму, которую он вложил в облигацию при покупке. Особенность состоит в том, что совокупность платежей, которые должен получить владелец облигации растянута во времени, и следовательно, все будущие денежные потоки необходимо продисконтировать к моменту времени, для которого производится оценка стоимости облигации. В качестве показателя дисконта необходимо принимать доходность аналогичных финансовых инструментов.
Математическая модель оценки денежной стоимости облигаций основана на дисконтировании денежных потоков, выплачиваемых на протяжении всего срока до погашения. Стоимость облигации в настоящий момент времени равна дисконтированной сумме всех денежных потоков, с ней связанных:
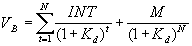 , (5.1) , (5.1)
М — номинальная стоимость облигаций, она же — стоимость в момент погашения;
INT — годовой процентный платеж;
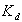 — доходность на рынке ссудного капитала аналогичных облигаций (используется в качестве показателя дисконтирования). — доходность на рынке ссудного капитала аналогичных облигаций (используется в качестве показателя дисконтирования).
Пример 1. Пусть выпущена облигация со сроком погашения через 20 лет. Номинал облигации равен $ 1,000, а годовая процентная ставка, определяющая величину годового процентного платежа, составляет 14 процентов. Средняя процентная ставка на рынке облигаций данного типа составляет также 14%. Необходимо найти оценку стоимости облигации?
Поскольку по условию процентный платеж производится один раз в год, величина этого платежа составляет $140. На рынке ссудного капитала доходность составляет 14%. Следовательно для оценки стоимости облигации мы должны привести к настоящему времени все ежегодные процентные платежи и выплату номинала в конце двадцатого года. Воспользовавшись формулой (5.1), получим
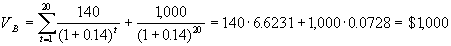 . .
Пусть прошло 5 лет, а процентная ставка на рассматриваемом рынке ссудного капитала не изменилась. Сколько будет стоить данная облигация? Для ответа на этот вопрос нужно найти современную стоимость всех оставшихся платежей, включая номинал облигации, который должен быть выплачен инвестору через 15 лет. По аналогии получим:
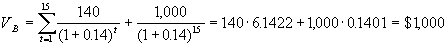 . .
Стоимость облигации закономерно осталась равной ее номиналу, так как ситуация на рынке не изменилась. Ясно, что такая ситуация сохранится на протяжении всего срока до погашения облигации.
Предположим теперь, что средняя рыночная ставка увеличилась на 2 процента и составляет 16%, до погашения облигации осталось 15 лет. В этом случае доходность данной облигации ниже средней по рынку, и следовательно рыночная цена облигации должна уменьшиться. Это подтверждается расчетами:
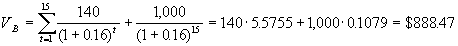 . .
Если теперь рассмотреть противоположную ситуацию, когда средняя по рынку процентная ставка уменьшилась на 2 процента и составляет 12%, то следует ожидать повышение рыночной цены этой облигации, так как она приносит доходность большую, чем средняя по рынку. В самом деле
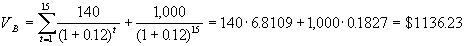 . .
Легко проверить, что для обоих рассмотренных случаев, если ситуация на рынке остается без изменения (т.е. сохраняется 16% или 12%), стоимость облигации приближается к номинальному значению.
Если выплата процентов по облигации производится два раза в год, то расчетная формула изменится:
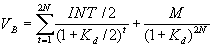 , ,
т.е. дисконтировать необходимо все полугодовые выплаты в соответствии с полугодовой процентной ставкой.
Для условий предыдущего примера, когда процентная ставка составляет 12% и до погашения остается 15 лет при полугодовой выплате процентов, получим
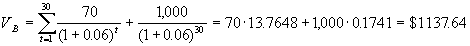 . .
В этом случае стоимость облигации оказалась несколько выше, так как процентные платежи инвестор получает более часто. И следовательно, при возрастании стоимости облигации этот эффект должен сказаться на курсовой стоимости облигации.
Рассмотрим теперь случай краткосрочных (длительностью один год) облигаций, который более характерен для экономики Украины. Пусть номинальная стоимость облигации составляет 100 гривен со сроком погашения через 364 дня. Процентные выплаты производятся через каждые 91 день в размере 25 гривен, причем последний купон выплачивается в момент погашения облигации одновременно с номиналом. Пусть квартальная доходность аналогичных долговых обязательств (для ориентира можно выбрать облигации внутреннего государственного займа) составляют 10%. В соответствии с формулой (5.1) получим:
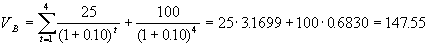 . .
Если по истечению одного квартала процентная ставка драматично увеличилась до 18 процентов, то стоимость облигации составит
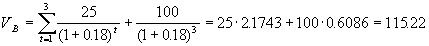 . .
Такое изменение представляется закономерным и отражает реальную рыночную ситуацию. В частности, если положение вследствие всплеска инфляции резко ухудшится и квартальная процентная ставка составит 32%, то облигации будут продаваться ниже своего номинала.
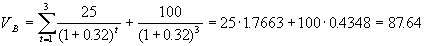 . .
Обратимся теперь к дисконтным облигациям, которые также имеют номинальную стоимость, которая выплачивается инвестору в момент погашения облигации. В процессе эмиссии такие облигации продаются со скидкой (дисконтом). Величина скидки определяется процентной ставкой по данной облигации. Дальнейшее изучение оценки стоимости такой облигации проведем с помощью конкретного примера.
Пример 2. Предприятие А в день эмиссии приобрело по цене 82 гривни за штуку пакет дисконтных государственных облигаций с периодом обращения 365 дней и номинальной стоимость к погашению 100 гривень. Доходность этого финансового инструмента на момент эмиссии составляла
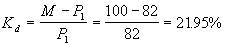 . .
Через 165 дней, или за 200 дней до погашения облигации предприятие А решило реализовать на рынке этот пакет ценных бумаг, так как ему срочно понадобились деньги. Цена продажи была определена следующим образом:
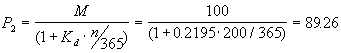 . .
Продавец дисконтировал стоимость облигации к погашению (100 гривень), использовав в качестве дисконтной ставки (21.95%) тот уровень доходности, который обеспечивал ему данный финансовый инструмент. Смысл этого расчета заключается в том, чтобы разделить первоначальную величину дисконтного дохода (100 — 82 = 18 гривень) между продавцом и покупателем в соответствии с продолжительностью периодов владения финансовым активом. Продавец владел активом 165 дней из 365, и он желает получить свою часть дисконтного дохода: 89.26 — 82 = 7.26 гривень с одной облигации. Покупателю (по мнению продавца) должна достаться та часть дисконтного дохода, которая соответствует 200 дням владения финансовым инструментом:
100 — 89.26 = 10.74 гривень.
Институциональные инвесторы, желающие приобрести эти государственные облигации, считали предложенную цену завышенной, так как доминирующая процентная ставка на рынке аналогичных финансовых ресурсов на момент продажи составила 23 процента. Оценка стоимости облигаций в этом случае составляет
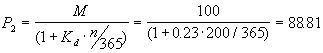 , ,
т.е. стала закономерно ниже. Предприятию А пришлось удовлетвориться данной ценной своего финансового ресурса.
Характеризуя этот факт, современная финансовая теория справедливо называет прошлые затраты "мертвыми", т.е. не имеющими значения при обосновании финансовых решений.
5. 2. Оценка стоимости обыкновенных акций предприятия
В соответствии с принятыми нормами выпуска обыкновенных акций сумма выплачиваемых дивидендов зависит от результатов деятельности предприятия в соответствующем периоде времени, обычно в течение года. Тем не менее оценка стоимости обыкновенных акций предполагает некоторый поток дивидендов, которые при оценке стоимости играют такую же роль, как процентные платежи при оценке облигации. Только в отличие от облигаций этот поток является бесконечным и не предполагается возврата исходной инвестиции. С учетом всего отмеченного выше оценка стоимости обыкновенной акции осуществляется по формуле
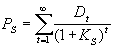 , (5.2) , (5.2)
где Dt — величина дивиденда, выплачиваемого в t-ом году,
Ks- показатель дисконта, с помощью которого осуществляется приведение дивидендных выплат к настоящему моменту времени.
Проблемы, связанные с оценкой стоимости акций, заключаются в прогнозе дивидендов и в оценке показателя дисконта. Рассмотрим каждую из них в отдельности.
Совершенно очевидно, что предприятие не в состоянии осуществить индивидуальный прогноз дивидендов на всем бесконечном периоде. Поэтому на практике этот период разбивают на две части, первая из которых составляет несколько лет (обычно не более пяти), в течение которых существует возможность составить более или менее правдоподобный прогноз дивидендных выплат. Вторая часть — это весь оставшийся бесконечный период времени, для которого делается предположение о том, что
- дивиденды сохраняют неизменное значение, равное величине последнего спрогнозированного дивиденда, вошедшего в первый период, или
- предполагается некоторый постоянный годовой прирост дивидендов, определяемый величиной процентного роста g.
В дальнейшем оценка стоимости акции — это дело техники дисконтирования спрогнозированной совокупности дивидендов.
Результирующая формула для оценки стоимости обыкновенных акций может быть записана следующим образом:
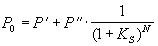 , (5.3) , (5.3)
где 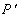 — дисконтированное значение прогнозируемых дивидендов на первом (конечном) промежутке времени продолжительностью N лет, — дисконтированное значение прогнозируемых дивидендов на первом (конечном) промежутке времени продолжительностью N лет,
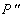 — дисконтированное значение последующей бесконечной серии дивидендов, приведенное к моменту времени, соответствующему концу N -ого года. — дисконтированное значение последующей бесконечной серии дивидендов, приведенное к моменту времени, соответствующему концу N -ого года.
Для расчета первой компоненты необходимо просто продисконтировать все величины дивидендов, спланированные к выплате в течение первых N лет:
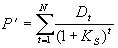 . (5.4) . (5.4)
Расчет второй компоненты для неизменных дивидендов производится по формуле дисконтирования бесконечных дивидендов
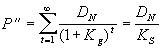 . (5.5) . (5.5)
Если предполагается рост дивидендов с темпом g, то необходимо воспользоваться формулой Гордона, которая является обобщением формулы (5.5) и имеет для рассматриваемой задачи следующий вид:
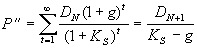 . (5.6) . (5.6)
Задача оценки стоимости обыкновенных акций решается однозначно при известном показателе дисконта. Для конкретного предприятия он определяется с учетом степени рискованности инвестирования в это предприятие. Взаимосвязь риска и доходности инвестиций будет обстоятельно рассмотрена в следующей публикации. Сейчас же только отметим, что для определения доходности акций Ks нужно иметь сравнительные данные данного предприятия и фондового рынка в целом. И естественно нужно иметь этот фондовый рынок. В современных условиях Украины говорить об этом, как о свершившемся факте, пока еще очень рано, и поэтому приходится использовать более упрощенные и приближенные подходы.
Один из таких подходов состоит в следующем. В качестве показателя доходности Ks используется оценка доходности предприятия, наблюдаемая в течение последнего года. Эта доходность определяется с помощью двух компонент:
- доходности инвестора, получаемой в виде дивидендов (величина дивиденда, выплаченная за последний год, деленная на рыночную стоимость акции), и
- доходность инвестора, связанная с увеличением курсовой стоимости акции (приращение курсовой стоимости акции за год, деленное на курсовую стоимость в начале года).
Сложив приведенные выше компоненты, мы получим доходность акции.
Пример 3. Предприятие выплатило по дивидендам 0.52 гривни в виде дивидендов за последний год. В течение ближайших трех лет предприятие планирует увеличивать дивиденды на 8 процентов, а в дальнейшем темп роста дивидендов должен составить 4 процента. Необходимо оценить стоимость акции при условии, что доходность акций оценена на уровне 15%.
Прежде всего оценим величины дивидендов, выплачиваемые в ближайшие три года:
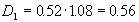 , ,
 , ,
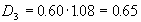 . .
Величина дивиденда, планируемая к выплате в конце четвертого года, должна составить
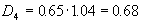 . .
Воспользовавшись формулами (5.4) и (5.6), получим
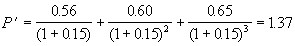 . .
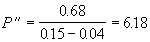 . .
Теперь осталось воспользоваться формулой (5.3):
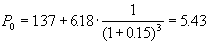 грн. грн.
5. 3. Составление графиков возврата долгосрочных кредитов
В процессе разработки инвестиционных проектов могут привлекаться кредитные ресурсы, которые возвращаются в процессе реализации проекта. Сумма кредита обычно возвращается постепенно в течение его срока. Различают два типа порядка погашения:
- периодическими взносами ("воздушный шар");
- "амортизационное" (постепенная выплата равномерными взносами).
Погашение периодическими взносами. При этом способе основную сумму кредита выплачивают на протяжении всего срока кредита. Однако порядок погашения таков, что по окончании срока от суммы кредита остается достаточно значительная доля, подлежащая погашению.
Пример 4. Представим себе, что предприятие получает кредит в сумме 100,000 грн. сроком на 5 лет. Платежи в счет погашения кредита вносятся ежегодно в сумме 12,000 грн. плюс процент. Таким образом, в конце 5-летнего периода, уже осуществлены четыре платежа по 12,000 грн. (всего 48,000 грн.), и остается невыплаченной сумма в 52,000 грн., которую полностью выплачивают по окончании срока кредита. Такой порядок погашения проиллюстрирован следующей таблицей.
|
Год |
Начальный баланс долга |
Погашение долга |
Проценты |
Годовая выплата |
Конечный баланс долга |
|
1 |
100,000 |
12,000 |
60,000 |
72,000 |
88,000 |
|
2 |
88,000 |
12,000 |
52,800 |
64,800 |
76,000 |
|
3 |
76,000 |
12,000 |
45,600 |
57,600 |
64,000 |
|
4 |
64,000 |
12,000 |
38,400 |
50,400 |
52,000 |
|
5 |
52,000 |
52,000 |
31,200 |
83,200 |
— |
|
Итог |
|
100,000 |
228,000 |
|
|
Заметим, что проценты начисляются исходя из величины начального на текущий год баланса долга.
Кредит может быть погашен равными взносами. Процент выплачивают по непогашенной части долга, поэтому общая сумма взноса по погашению основной суммы и процента уменьшается по мере того, как истекает срок кредита. Взносы по погашению основной суммы не изменяются. Однако каждая следующая процентная выплата меньше предыдущей, так как остающаяся непогашенной часть основной суммы уменьшается.
Если предприятие планирует погашать долг равными порциями, то график обслуживания долга будет иметь вид:
|
Год |
Начальный баланс долга |
Погашение долга |
Проценты |
Годовая выплата |
Конечный баланс долга |
|
1 |
100,000 |
20,000 |
60,000 |
80,000 |
80,000 |
|
2 |
80,000 |
20,000 |
48,000 |
68,000 |
60,000 |
|
3 |
60,000 |
20,000 |
36,000 |
56,000 |
40,000 |
|
4 |
40,000 |
20,000 |
24,000 |
44,000 |
20,000 |
|
5 |
20,000 |
20,000 |
12,000 |
32,000 |
— |
|
Итог |
|
100,000 |
180,000 |
|
|
При сравнении с предыдущей таблицей приходим к выводу о том, что сумма процентных платежей в первом варианте закономерно выше.
'Амортизационное" погашение кредита. При "амортизационном" погашении основную сумму кредита выплачивают постепенно на протяжении срока кредита. Платежи осуществляют равными суммами регулярно (как правило, ежемесячно, ежеквартально или раз в полгода), и они включают определенную часть суммы кредита и процент. Вместе с последним взносом сумму кредита погашают. Этот принцип используют при ипотечном кредите. Многие западные кредитные инвесторы используют эту схему в качестве базового графика возврата долга предприятием-заемщиком.
Пример 5. Кредитный инвестор предлагает предприятию кредит под 12 процентов годовых срок на 4 года при полугодовой схеме возврата долга. Предприятие планирует привлечь 800,000 американских долларов. Необходимо рассчитать график обслуживания долга.
Прежде всего необходимо вычислить величины полугодовой выплаты. При расчете этой суммы используется концепция стоимости денег во вемени. Применительно к данному вопросу она заключается в том, что приведенная к настоящему моменту сумма всех платежей должна быть равной сумме кредита.
Если PMT — неизвестная величина годовой выплаты, а S — величина кредита, то при процентной ставке кредита і и количестве периодических платежей n величина PMT может быть вычислена с помощью уравнения:
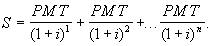
Решение этого уравнения можно произвести с помощью финансовых таблиц или электронного процессора EXCEL. Для данного примера сумма годового платежа равна 128,829. Таблица обслуживания долга имеет вид:
|
Год |
Начальный баланс долга |
Погашение долга |
Проценты |
Годовая выплата |
Конечный баланс долга |
|
1 |
800,000 |
80,829 |
48,000 |
128,829 |
719,171 |
|
2 |
719,171 |
85,678 |
43,150 |
128,829 |
633,493 |
|
3 |
633,493 |
90,819 |
38,010 |
128,829 |
542,674 |
|
4 |
542,674 |
96,268 |
32,560 |
128,829 |
446,405 |
|
5 |
446,405 |
102,044 |
26,784 |
128,829 |
344,361 |
|
6 |
344,361 |
108,167 |
20,662 |
128,829 |
236,194 |
|
7 |
236,194 |
114,657 |
14,172 |
128,829 |
121,537 |
|
8 |
121,537 |
121,537 |
7,292 |
128,829 |
0 |
|
Итог |
|
800,000 |
230,630 |
|
|
Для сравнения приведем график обслуживания той же суммы кредита по схеме погашения основной части долга равными порциями:
|
Год |
Начальный баланс долга |
Погашение долга |
Проценты |
Годовая выплата |
Конечный баланс долга |
|
1 |
800,000 |
100,000 |
48,000 |
148,000 |
700,000 |
|
2 |
700,000 |
100,000 |
42,000 |
142,000 |
600,000 |
|
3 |
600,000 |
100,000 |
36,000 |
136,000 |
500,000 |
|
4 |
500,000 |
100,000 |
30,000 |
130,000 |
400,000 |
|
5 |
400,000 |
100,000 |
24,000 |
124,000 |
300,000 |
|
6 |
300,000 |
100,000 |
18,000 |
118,000 |
200,000 |
|
7 |
200,000 |
100,000 |
12,000 |
112,000 |
100,000 |
|
8 |
100,000 |
100,000 |
6,000 |
106,000 |
— |
|
Итог |
|
800,000 |
216,000 |
|
|
Поскольку суммарные процентные выплаты во второй схеме существенно меньше, может показаться, что этот график более выгоден. На самом деле обе схеме одинаковы в смысле "справедливости" взаимоотношений между кредитором и заемщиком, так как современное дисконтированное значение всех годовых платежей во второй схеме, как и первой, равно исходной сумме кредита 800,000.
Контрольные вопросы и задания
- На каком принципе базируется подход к оценке стоимости ценных бумаг предприятия?
- Каковы основные элементы купонных облигаций, используемые для расчета их стоимости?
- В чем состоит экономическая сущность оценки стоимости облигации?
- Запишите формулу для расчета стоимости купонной облигации.
- Как соотносится стоимость купонной облигации с ее номиналом, если рыночная процентная ставка выше номинальной?
- Как изменится стоимость облигации через три года после выпуска, если в течение этих трех лет рыночная процентная ставка не изменялась и была равной номинальной процентной ставке по облигации.
- Как влияет периодичность выплаты процентов (количество раз в году) по купонной облигации на расчет ее стоимости?
- Если облигация выпускается с процентной ставкой выше рыночной, то по какой цене следует ожидать ее продажу: выше номинала или ниже?
- Что такое дисконтная облигация?
- Как делится доход по дисконтной облигации между ее старым и новым владельцем в случае продажи облигации?
- Из чего надо исходить при определении цены покупки дисконтной облигации на вторичном рынке?
- Какие затраты называют "мертвыми" при рассмотрении стоимости ценных бумаг?
- Какая информация используется при расчете стоимости обыкновенных акций предприятия?
- Какой период принимается во внимание при расчете стоимости обыкновенных акций?
- Как отличаются модели расчета стоимости обыкновенных акций при неизменных прогнозируемых дивидендах и при возрастающих дивидендах?
- Какие два вида графиков погашения кредита используются в долгосрочном кредитовании?
- Как вычисляются процентные платежи при составлении графика обслуживания долга?
- Как рассчитать годовую сумму выплаты при амортизационном погашении кредита?
- Как изменится график погашения кредита, если кредитор предоставляет отсрочку от выплаты основной части долга на несколько периодов?
- Какая из двух схем погашения кредита более выгодна кредитору, а какая заемщику?
Задания
1. Вы заняли на четыре года $10000 под 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите величину годового платежа.
2. Какие условия предоставления кредита более выгодны банку: а) 28% годовых, начисление ежеквартальное; б) 30% годовых, начисление полугодовое?
3. Предприятие приобрело здание за $20000 на следующих условиях: а) 25% стоимости оплачивается немедленно; б) оставшаяся часть погашается равными годовыми платежами в течение 10 лет с начислением 12% годовых на непогашенную часть кредита по схеме сложных процентов. Определите величину годового платежа.
4. Оцените текущую стоимость облигации номиналом $1000, купонной ставкой 9% годовых и сроком погашения через 3 года, если рыночная норма прибыли равна 7%.
5. Вычислите текущую цену бессрочной облигации, если выплачиваемый по ней годовой доход составляет 100 тыс. грн., а рыночная доходность — 12%.
6. Вы приобретаете бескупонную государственную облигацию номиналом $5000, погашаемую через 25 лет. Какова ее текущая цена, если ставка банковского процента равна 15%?
7. Вычислите текущую стоимость облигации с нулевым купоном нарицательной стоимостью 100 грн. и сроком погашения 12 лет, если приемлемая норма прибыли составляет 14%.
8. Рассчитайте текущую стоимость привилегированной акции номиналом 100 грн. и величиной дивиденда 9% годовых, если рыночная норма прибыли 12%.
9. Последний выплаченный дивиденд по акции равен $1. Ожидается, что он будет возрастать в течение следующих трех лет с темпом 14%; затем темп прироста стабилизируется на величине 5%. Какова цена акции, если рыночная норма прибыли 15%.
10. Куплена акция за $50; прогнозируемый дивиденд текущего года составит $2. Ожидается, что в следующие годы этот дивиденд будет возрастать с темпом 10%. Какова приемлемая норма прибыли, использованная инвестором при принятии решения о покупке акции?
11. Четыре года назад компания А платила дивиденд в размере $0,80 на акцию. Последний выплаченный дивиденд составил $1,66. Ожидается, что такой же среднегодовой темп прироста дивидендов сохранится и в последующие пять лет, после чего темп прироста стабилизируется на уровне 8%. Текущая рыночная цена акции $30. Следует ли покупать эту акцию, если требуемая норма прибыли составляет 18%?
12. Последний выплаченный компанией А дивиденд равен $7, темп прироста дивидендов составляет 3% в год. Какова текущая цена акций компании, если коэффициент дисконтирования равен 12%?
13. Компания А не выплачивала дивиденды в отчетном году, но в следующем году планирует выплатить дивиденд в размере $5. В последующие годы ожидается постоянный рост дивидендов с темпом 6%. Какова текущая цена акций компании, если коэффициент дисконтирования равен 13%?
14. Облигация номиналом $500 с полугодовым начислением процентов и купонной ставкой 10% годовых будет погашена через 6 лет. Какова ее текущая цена, если рыночная норма прибыли: а) 8%; б) 10%; в) 12%?
ПРОДОЛЖЕНИЕ >>
|
 |
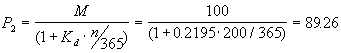 .
.
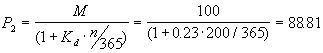 ,
,
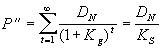 . (5.5)
. (5.5)