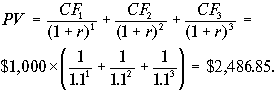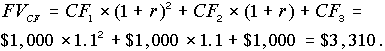>> ОГЛАВЛЕНИЕ
4. Финансово-математические основы инвестиционного проектирования
4. 1. Концепция стоимости денег во времени
В основе концепции стоимости денег во времени лежит следующий основной принцип: Доллар сейчас стоит больше, чем доллар, который будет получен в будущем, например через год, так как он может быть инвестирован и это принесет дополнительную прибыль. Данный принцип является наиболее важным положением во всей теории финансов и анализе инвестиций. На этом принципе основан подход к оценке экономической эффективности инвестиционных проектов.
Данный принцип порождает концепцию оценки стоимости денег во времени. Суть концепции заключается в том, что стоимость денег с течением времени изменяется с учетом нормы прибыльности на денежном рынке и рынке ценных бумаг. В качестве нормы прибыльности выступает норма ссудного процента или норма выплаты дивидендов по обыкновенным и привилегированным акциям.
Учитывая, что инвестирование представляет собой обычно длительный процесс, в инвестиционной практике обычно приходится сравнивать стоимость денег в начале их инвестирования со стоимостью денег при их возврате в виде будущей прибыли. В процессе сравнения стоимости денежных средств при их вложении и возврате принято использовать два основных понятия: настоящая (современная) стоимость денег и будущая стоимость денег.
Будущая стоимость денег представляет собой ту сумму, в которую превратятся инвестированные в настоящий момент денежные средства через определенный период времени с учетом определенной процентной ставки. Определение будущей стоимости денег связано с процессом наращения (compounding) начальной стоимости, который представляет собой поэтапное увеличение вложенной суммы путем присоединения к первоначальному ее размеру суммы процентных платежей. В инвестиционных расчетах процентная ставка платежей применяется не только как инструмент наращения стоимости денежных средств, но и как измеритель степени доходности инвестиционных операций.
Настоящая (современная) стоимость денег представляет собой сумму будущих денежных поступлений, приведенных к настоящему моменту времени с учетом определенной процентной ставки. Определение настоящей стоимости денег связано с процессом дисконтирования (discounting), будущей стоимости, который (процесс) представляет собой операцию обратную наращению. Дисконтирование используется во многих задачах анализа инвестиций. Типичной в данном случае является следующая: определить какую сумму надо инвестировать сейчас, чтобы получить например, $1,000 через 5 лет.
Таким образом, одну и ту же сумму денег можно рассматривать с двух позиций:
а) с позиции ее настоящей стоимости
б) с позиции ее будущей стоимости
Причем, арифметически стоимость денег в будущем всегда выше.
4. 2. Элементы теории процентов
В процессе анализа инвестиционных решений принято использовать сложные проценты. Сложным процентом называется сумма дохода, которая образуется в результате инвестирования денег при условии, что сумма начисленного простого процента не выплачивается в конце каждого периода, а присоединяется к сумме основного вклада и в следующем платежном периоде сама приносит доход.
Основная формула теории процентов определяет будущую стоимость денег:
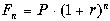 , (4.1) , (4.1)
где P — настоящее значение вложенной суммы денег,
F — будущее значение стоимости денег,
n — количество периодов времени, на которое производится вложение,
r — норма доходности (прибыльности) от вложения.
Простейшим способом эту формулу можно проинтерпретировать, как определение величины депозитного вклада в банк при депозитной ставке r (в долях единицы).
Существо процесса наращения денег не изменяется, если деньги инвестируются в какой-либо бизнес (предприятие). Главное, чтобы вложение денег обеспечивало доход, то есть увеличение вложенной суммы.
Пример 1. Банк выплачивает 5 процентов годовых по депозитному вкладу. Согласно формуле (4.1) $100, вложенные сейчас, через год станут
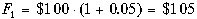 . .
Если вкладчик решает оставить всю сумму на депозите еще на один год, то к концу второго года объем его вклада составит
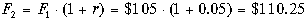 , ,
или по формуле (4.1)
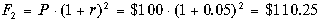 . .
Процесс наращения стоимости $100 по годам можно представить в виде таблицы или диаграммы:
|
Год |
Обозначение |
Стоимость денег |
|
0 |
P |
$100 |
|
1 |
F1 |
$105 |
|
2 |
F2 |
$110.25 |
|
3 |
F3 |
$115.76 |
|
4 |
F4 |
$121.55 |
|
5 |
F5 |
$127.63 |
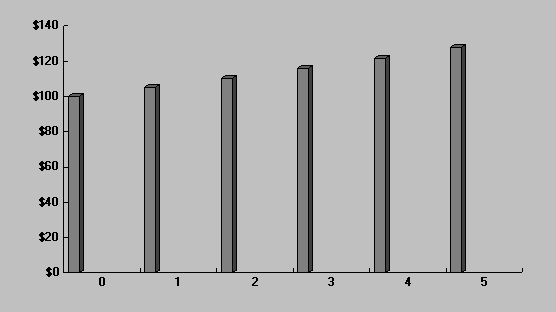
Следует отметить, что процесс наращения не является линейным.
Настоящее (современное) значение стоимости определенной будущей суммы денег определяется с помощью формулы
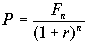 , (4.2) , (4.2)
которая является простым обращением формулы (4.1).
Пример 2. Пусть инвестор хочет получить $200 через 2 года. Какую сумму он должен положить на срочный депозит сейчас, если депозитная процентная ставка составляет 5%.
С помощью формулы (4.2) легко определить
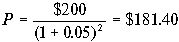 . .
Понятно, что формула (4.2) лежит в основе процесса дисконтирования. И в этом смысле величина r интерпретируется как ставка дисконта и часто называется просто дисконтом.
Рассмотренный в примере (4.2) случай можно интерпретировать следующим образом:
$181.40 и $200 — это два способа представить одну и ту же сумму денег в разные моменты времени — $200 через два года равносилен $181.40 сейчас.
Процесс дисконтирования наглядно можно продемонстрировать с помощью следующего графика:
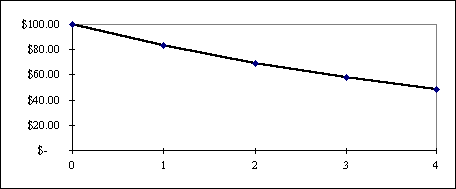
В анализе инвестиции величины (1+r)n и (1+r)-n часто называют соответственно множителями наращения и дисконтирования. Наращение и дисконтирование единичных денежных сумм удобно производить с помощью финансовых таблиц 1 и 3, помещенных в приложении. В этих таблицах содержатся множители наращения и дисконтирования, соответственно.
4. 3. Влияние инфляции при определении настоящей и будущей стоимости денег
В инвестиционной практике постоянно приходится считаться с корректирующим фактором инфляции, которая с течением времени обесценивает стоимость денежных средств. Это связано с тем, что инфляционный рост индекса средних цен вызывает соответствующее снижение покупательной способности денег.
При расчетах, связанных с корректировкой денежных потоков в процессе инвестирования с учетом инфляции, принято использовать два основных понятия
- номинальная сумма денежных средств,
- реальная сумма денежных средств.
Номинальная сумма денежных средств не учитывает изменение покупательной способности денег. Реальная сумма денежных средств — это оценка этой суммы с учетом изменения покупательной способности денег в связи с процессом инфляции.
В финансово-экономических расчетах, связанных с инвестиционной деятельностью, инфляция учитывается в следующих случаях:
- при корректировке наращенной стоимости денежных средств,
- при формировании ставки процента (с учетом инфляции), используемой для наращения и дисконтирования,
- при прогнозе уровня доходов от инвестиций, учитывающих темпы инфляции.
В процессе оценки инфляции используются два основных показателя:
- темп инфляции Т, характеризующий прирост среднего уровня цен в рассмотренном периоде, выражаемый десятичной дробью,
- индекс инфляции I (изменение индекса потребительских цен), который равен 1+Т.
Корректировка наращенной стоимости с учетом инфляции производится по формуле
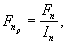 (4.3) (4.3)
где 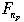 — реальная будущая стоимость денег, — реальная будущая стоимость денег,
Fn — номинальная будущая стоимость денег с учетом инфляции.
Здесь предполагается, что темп инфляции сохраняется по годам.
Если r — номинальная ставка процента, которая учитывает инфляцию, то расчет реальной суммы денег производится по формуле:
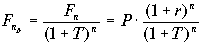 , (4.4) , (4.4)
то есть номинальная сумма денежных средств снижается в (1+Т)n раза в соответствии со снижением покупательной способности денег.
Пример 3. Пусть номинальная ставка процента с учетом инфляции составляет 50%, а ожидаемый темп инфляции в год 40%. Необходимо определить реальную будущую стоимость объема инвестиций 200,000 грн.
Подставляем данные в формулу (4.4), получаем
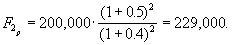
Если же в процессе реального развития экономики темп инфляции составит 55%, то
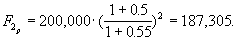
Таким образом, инфляция "съедает" и прибыльность и часть основной суммы инвестиции, и процесс инвестирования становится убыточным.
В общем случае при анализе соотношения номинальной ставки процента с темпом инфляции возможны три случая:
- r = T :
наращение реальной стоимости денежных средств не происходит, так как прирост их будущей стоимости ПОГЛОЩАЕТСЯ инфляцией
- r > T
: реальная будущая стоимость денежных средств возрастает несмотря на инфляцию
- r < T
: реальная будущая стоимость денежных средств снижается, то есть процесс инвестирования становится УБЫТОЧНЫМ.
Взаимосвязь номинальной и реальной процентной ставок.
Пусть инвестору обещана реальная прибыльность его вложений в соответствии с процентной ставкой 10 %. Это означает, что при инвестировании 1,000 грн. через год он получит 1,000 х (1+0.10) = 1,100 грн. Если темп инфляции составляет 25 %, то инвестор корректирует эту сумму в соответствии с темпом: 1,100 х (1+0.25) = 1,375 грн. Общий расчет может быть записан следующим образом
1,000 х (1+0.10) х (1+0.25) = 1,375 грн.
В общем случае, если rр - реальная процентная ставка прибыльности, а Т — темп инфляции, то номинальная (контрактная) норма прибыльности запишется с помощью формулы
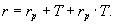
Величина rз + rзT имеет смысл инфляционной премии.
Часто можно встретить более простую формулу, которая не учитывает "смешанный эффект" при вычислении инфляционной премии
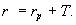
Эту упрощенную формулу можно использовать только в случае невысоких темпов инфляции, когда смешанный эффект пренебрежимо мал по сравнению с основной компонентой номинальной процентной ставки прибыльности.
Отношение к инфляции в реальной практике. Прогнозирование темпов инфляции очень сложный процесс, протекающий на фоне большого количества неопределенностей. Это особенно характерно для стран с неустойчивым экономическим положением. Кроме того, темпы инфляции в отдельные периоды в значительной степени подвержены влиянию субъективных факторов, слабо поддающихся прогнозированию. Поэтому один из наиболее реально значимых подходов может состоять в следующем: стоимость инвестируемых средств и суммы денежных средств, обеспечивающих возврат, пересчитываются из национальной валюты в одну из наиболее устойчивых твердых валют (доллар США, фунт стерлингов Великобритании, немецкие марки). Пересчет осуществляется по биржевому курсу на момент проведения расчетов. Процесс наращения и дисконтирования производится в данном случае не принимая во внимание инфляцию. Конкретная процентная ставка определяется исходя из источника инвестирования. Например, при инвестировании за счет кредитов коммерческого банка в качестве показателя дисконта принимается процентная ставка валютного кредита этого банка.
4. 4. Наращение и дисконтирование денежных потоков
Поскольку процесс инвестирования, как правило, имеет большую продолжительность в практике анализа эффективности капитальных вложений, обычно приходится иметь дело не с единичными денежными суммами, а с потоками денежных средств.
Вычисление наращенной и дисконтированной оценок сумм денежных средств в этом случае осуществляется путем использования соответствующих формул (4.1) и (4.2) для каждого элемента денежного потока.
Денежный поток принято изображать на временной линии в одном из двух способов:
А.
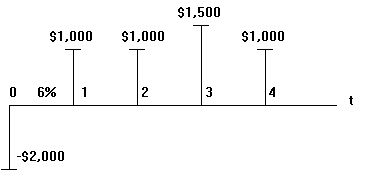
В.
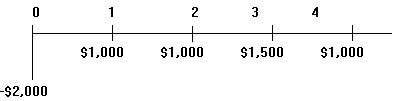
Представленный на рисунке денежный поток состоит в следующем: в настоящее время выплачивается (знак "минус") $2,000, в первый и второй годы получено $1,000, в третий — $1,500, в четвертый — снова $1,000.
Элемент денежного потока принято обозначать CFk (от Cash Flow), где k — номер периода, в который рассматривается денежный поток. Настоящее значение денежного потока обозначено PV ( Present Value), а будущее значение — FV ( Future Value).
Используя формулу (4.1), для всех элементов денежного потока от 0 до n получим будущее значение денежного потока
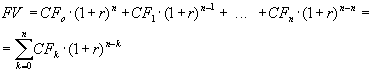 (4.5) (4.5)
Пример 4. После внедрения мероприятия по снижению административных издержек предприятие планирует получить экономию $1,000 в год. Сэкономленные деньги предполагается размещать на депозитный счет (под 5 % годовых) с тем, чтобы через 5 лет накопленные деньги использовать для инвестирования. Какая сумма окажется на банковском счету предприятия?
Решим задачу с использованием временной линии.
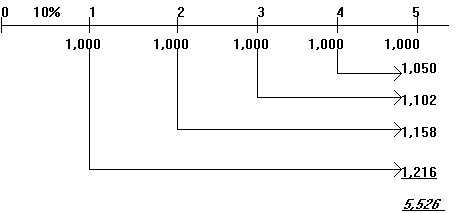
Таким образом через 5 лет предприятие накопит $5,526, которые сможет инвестировать.
В данном случае денежный поток состоит из одинаковых денежных сумм ежегодно. Такой поток называется аннуитетом. Для вычисления будущего значения аннуитета используется формула
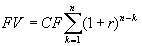 , (4.6) , (4.6)
которая следует из (4.5) при CFk = const и CF0 = 0.
Расчет будущего значения аннуитета может производиться с помощью специальных финансовых таблиц. Фрагмент этих таблиц помещен в приложении (таблица 2). В частности, с помощью таблицы 2 при r = 5% и n = 5 получаем множитель 5,526, который соответствует результату расчета примера.
Дисконтирование денежных потоков осуществляется путем многократного использования формулы (4.2), что в конечном итоге приводит к следующему выражению:
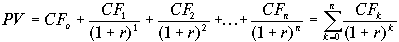 (4.7) (4.7)
Пример 5. Рассмотрим денежный поток с неодинаковыми элементами CF1=100, CF2=200, CF3=200, CF4=200, CF5=200, CF6=0, CF7=1,000, для которого необходимо определить современное значение (при показателе дисконта 6%). Решение проводим с помощью временной линии:
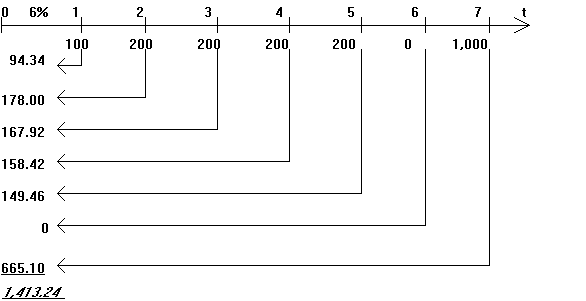
Вычисление дисконтированных значений отдельных сумм можно производить путем использования таблицы 3, помещенной в приложении
Дисконтирование аннуитета (CFj = const) осуществляется по формуле
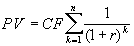 (4.8) (4.8)
Для расчета настоящего (современного) значения аннуитета может быть использована таблица 4 приложения.
Пример 6. Предприятие приобрело облигации муниципального займа, которые приносят ему доход $15,000, и хочет использовать эти деньги для развития собственного производства. Предприятие оценивает прибыльность инвестирования получаемых каждый год $15,000 в 12 %. Необходимо определить настоящее значение этого денежного потока.
Решение проведем с помощью таблицы:
|
Год |
Множитель при 12%
дисконтирования |
Поток денег |
Настоящее
значение |
|
1 |
0.893 |
$15,000 |
$13,395 |
|
2 |
0.797 |
$15,000 |
$11,955 |
|
3 |
0.712 |
$15,000 |
$10,680 |
|
4 |
0.636 |
$15,000 |
$9,540 |
|
5 |
0.567 |
$15,000 |
$8,505 |
| |
3.605 |
$75,000 |
$54,075 |
По результатам расчетов мы видим, что
- дисконтированное значение денежного потока существенно меньше арифметической суммы элементов денежного потока,
- чем дальше мы заходим во времени, тем меньше настоящее значение денег: $15,000 через год стоят сейчас $13,395; $15,000 через 5 лет стоят сейчас $8,505.
Задача может быть решена также с помощью таблицы 4 приложения. При r = 12% и n = 5 по таблице находим множитель дисконтирования 3.605.
Современное значение бесконечного (по времени) потока денежных средств определяется по формуле:
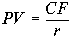 , (4.9) , (4.9)
которая получается путем суммирования бесконечного ряда, определяемого формулой (4.8) при 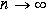 . .
4.5. Сравнение альтернативных возможностей вложения денежных средств с помощью техники дисконтирования и наращения
Техника оценки стоимости денег во времени позволяет решить ряд важных задач сравнительного анализа альтернативных возможностей вложения денег. Рассмотрим эту возможность на следующем примере.
Пример 7. Комплексное пояснение к временной стоимости денег. Рассмотрим поток $1,000, который генерируется какой либо инвестицией в течение 3 лет. Расчетная норма прибыльности инвестирования денежных средств предприятия составляет 10 %.
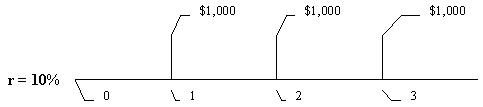
Попытаемся последовательно ответить на ряд вопросов, связанных с различными ситуациями относительно этого потока и его использования.
Вопрос 1. Какова современная стоимость этого потока?
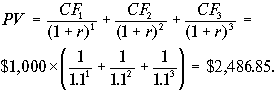
Вопрос 2. Какова будущая стоимость $2,486.85 на конец 3 года? (то есть если бы мы вложили деньги в банк под r = 10% годовых)?
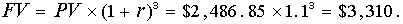
Вопрос 3. Какова будущая стоимость потока денежных средств на конец 3-го года?
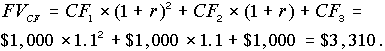
Мы получили одинаковые ответы на второй и третий вопросы. Вывод очевиден: если мы инвестируем в какой-либо бизнес $2,486.85 и эта инвестиция генерирует заданный поток денег $1,000, $1,000, $1,000, то на конец 3-го года мы получим ту же сумму денег $3,310, как если бы просто вложили $2,486.85 в финансовые инструменты под 10% годовых.
Пусть теперь величина инвестиции составляет $2,200, а генерируемый поток такой же, что приводит к концу 3-го года к $3,310.
Инвестирование $2,200 в финансовые инструменты под 10% даст, очевидно, 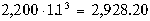 . Значит нам более выгодно инвестировать в данном случае в реальный бизнес, а не в финансовые инструменты. . Значит нам более выгодно инвестировать в данном случае в реальный бизнес, а не в финансовые инструменты.
Вопрос 4. Как изменится ситуация, если норма прибыльности финансового вложения денег r станет выше, например 12%.
По-прежнему мы инвестируем $2,486.85 в бизнес, и это приводит к потоку денежных средств $1,000 каждый год в течение 3-х лет. Современное значение этого потока
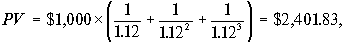
уменьшилось и стало меньше исходной суммы инвестиций $2,486.85.
Сравним будущее значение исходной суммы $2,486.85 и потока денежных средств, который генерирует инвестирование этой суммы в бизнес:
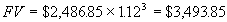 ; ;
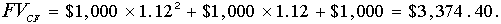
Выводы, которые можно сделать на основе сравнения этих значений таковы:
a) инвестирование суммы $2,486.85 в финансовые инструменты под 12% годовых приведет к $3,493.85 через 3 года,
б) инвестирование суммы $2,486.85 в бизнес, который генерирует денежный поток $1,000 каждый год в течение 3-х лет, приведет к $3,374.40 к концу 3-го года.
Очевидно, что при норме прибыльности 12% инвестировать в бизнес не выгодно.
Данный вывод имеет простое экономическое объяснение. Дело в том, что инвестирование денег в финансовые инструменты начинает приносить доход сразу же, начиная с первого года. В то же время, инвестирование денег в реальные активы позволяет получить первую $1,000 только к концу первого года, и она приносит финансовый доход только в течение оставшихся двух лет. Другими словами, имеет место запаздывание сроков начала отдачи в случае инвестирования реальные активы по сравнению с инвестицией в финансовые инструменты. И если при норме прибыльности 10 процентов оба варианта вложения денег равносильны в смысле конечной суммы "заработанных" денег, то увеличение нормы прибыльности делает инвестицию в финансовые инструменты более выгодной.
Возвратимся к количественному сравнению эффективности альтернативного вложения денег. Рассмотрим, насколько выгоднее вкладывать деньги в финансовые инструменты по сравнению с реальными инвестициями в двух временных точках: момент времени "сейчас" и конец третьего года.
В настоящее время поток денежных средств от реальной инвестиции составляет $2,401.83 при исходной инвестиции $2,486.85. Значит финансовая инвестиция более выгодна на $85. К концу третьего года финансовая инвестиция принесет $3,493.85, а реальная инвестиция — $3,374.40. Разница составляет $119.45. Существенно подчеркнуть, что это различие также подчиняется концепции стоимости денег во времени, т.е. продисконтировав $119.45 при 12 процентах мы закономерно получим $85.
Контрольные вопросы и задания
- Сформулируйте основной принцип стоимости денег во времени.
- В чем экономический смысл концепции стоимости денег во времени?
- Что понимается под наращением и дисконтированием денег?
- Перечислите четыре основные элемента, связанные между собой в концепции стоимости денег во времени.
- В чем экономический смысл нормы доходности инвестирования денег?
- Запишите основную формулу теории сложных процентов.
- Как изменяется будущая стоимость денег при увеличении продолжительности инвестирования?
- Сформулируйте пример практического использования современного значения денег.
- Какая стоимость денег является реальной: современная или будущая?
- Как следует корректировать ожидаемые денежные потоки в связи с инфляцией?
- Какие основные показатели инфляции используются при корректировке будущей стоимости денег?
- Как имея реальную доходность инвестиций и годовой темп инфляции подсчитать номинальную доходность инвестиций?
- Когда процесс инвестирования становится невыгодным?
- Когда процесс инвестирования становится убыточным?
- Что такое смешанный эффект при сопоставлении нормы доходности и темпа инфляции?
- Как производится процесс наращения и дисконтирования денежных потоков?
- Какой денежный поток называется аннуитетом?
- Как определить современное и будущее значения аннуитета?
- Что такое бесконечный аннуитет и как рассчитать его современное значение?
- Как устроены и зачем используются финансовые таблицы?
- Если сравнительная эффективность вложения в реальные активы и финансовые инструменты одинакова, то как она изменится при увеличении нормы доходности?
Задания.
1. Предположим Вы купили шестилетний 8-ми процентный сберегательный сертификат стоимостью $1,000. Если проценты начисляются ежегодно, какую сумму Вы получите по окончанию контракта?
Решение.
Используем формулу наращения денег, т.е. определяем будущую стоимость $1,000 через 6 лет при 8 процентах годовой прибыли:
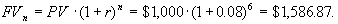
Такой же результат получается с помощью финансовой таблицы 1 прил. Проверьте.
2. Финансовый менеджер предприятия предложил Вам инвестировать Ваши $5,000 в его предприятие, пообещав возвратить Вам $6,000 через два года. Имея другие инвестиционные возможности, Вы должны выяснить, какова процентная ставка прибыльности предложенного Вам варианта.
Решение.
Используем основную формулу наращения денег:
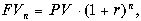
откуда следует
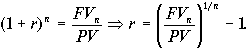
В нашем случае
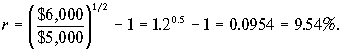
Ясно, что если кто-либо предложит Вам инвестировать Ваши деньги под, хотя бы, 10 процентов годовых, Вы отклоните предложение получить $6,000 через два года, вложив сейчас $5,000.
3. Вам предлагают инвестировать деньги с гарантией удвоить их количество через пять лет. Какова процентная ставка прибыльности такой инвестиции?
Решение.
Используем основную формулу предыдущей задачи, учитывая, что будущее значение какой-либо суммы через пять лет FV5 и ее современное значение PV относятся как 2:1.
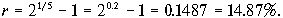
4. Предприятие собирается приобрести через три года новый станок стоимостью $8,000. Какую сумму денег необходимо вложить сейчас, чтобы через три года иметь возможность совершить покупку, если процентная ставка прибыльности вложения составляет
а) 10 процентов?
б) 14 процентов?
Решение.
По условию задачи мы должны определить современное значение стоимости станка $8,000 при ставке дисконта 10 процентов. Используем формулу дисконтирования:
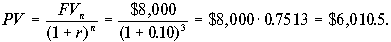
Аналогично для случая б):
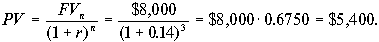
Закономерно, что во втором случае сумма вклада получилась меньше.
5. Проведя усовершенствование технологического процесса предприятие в течение пяти последующих лет планирует получение ежегодное увеличение денежного дохода на $10,000. Эти деньги оно собирается немедленно вкладывать под 10 процентов годовых, желая через пять лет накопить сумму для приобретения нового оборудования. Какую сумму денег предприятие получит через пять лет?
Решение.
По условию задачи предприятие планирует получить аннуитет $10,000 в течение пяти лет. Для определения суммы накопленных денег необходимо вычислить будущее значение пятилетнего аннуитета при процентной ставке наращения 10 процентов. Используем формулу будущего значения аннуитета:
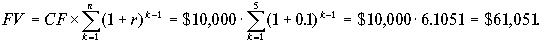
Такое же значение мы получаем, использовав финансовую таблицу для будущего значения аннуитета $1
6. Предприятие располагает $160,000 и предполагает вложить их в собственное производство, получая в течение четырех последующих лет ежегодно $50,000. В то же время предприятие может купить на эту сумму акции одной солидной корпорации, приносящие 12 процентов годовых. Какой вариант Вам представляется более приемлемым, если считать что более выгодной возможностью вложения денег (чем под 12 процентов годовых) предприятие не располагает?
Решение.
Для ответа на вопрос можно воспользоваться двумя способами рассуждения. Сравним будущее наращенное значение аннуитета $50,000 при процентной ставке 12 процентов с будущим значением альтернативного вложения всей суммы $160,000 при той же процентной ставке:
- будущее значение аннуитета —
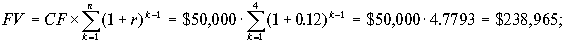
- будущее значение $160,000 —
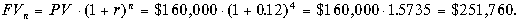
Результаты расчетов говорят о том, что покупка акций более выгодна, чем вложение этой же суммы денег в собственное производство.
Возможен другой подход к решению задачи, использующий приведение денежных потоков к настоящему времени. Этот подход более распространен в практике, поскольку он проще. В данном случае мы просто определяем настоящее значение аннуитета $50,000 при показателе дисконтирования 12 процентов:
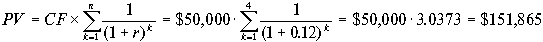 . Сравнивая полученное значение с суммой имеющихся в настоящее время денежных средств $160,000, приходим к такому же выводу: вкладывать деньги в акции солидной компании более выгодно. . Сравнивая полученное значение с суммой имеющихся в настоящее время денежных средств $160,000, приходим к такому же выводу: вкладывать деньги в акции солидной компании более выгодно.
Кто-либо может заметить, что численное значение различия альтернативных вариантов вложения в настоящее время $160,000 — $151,865 = $8,135 существенно меньше численного различия через четыре года $251,760 -$238,965 = $12,795. Это закономерно ввиду феномена стоимости денег во времени: если мы дисконтируем $12,795 на четыре года при показателе дисконта 12%, то получим $8,131. Отсутствие абсолютного совпадения объясняется только погрешностью расчетов, связанной округлением долларовых сумм до целых значений.
7. Предприятие рассматривает два альтернативных проекта капитальных вложений приводящих к одинаковому суммарному результату в отношении будущих денежных доходов:
|
Год |
Проект 1 |
Проект 2 |
|
1 |
$3,000 |
$6,000 |
|
2 |
$4,000 |
$4,000 |
|
3 |
$5,000 |
$5,000 |
|
4 |
$6,000 |
$3,000 |
|
Всего |
$ |
$ |
Оба проекта имеет одинаковый объем инвестиций. Предприятие планирует инвестировать полученные денежные доходы под 18 процентов годовых. Сравните современные значения полученных денежных доходов.
Решение.
Вычислим современные значения последовательностей денежных доходов по каждому проекту, дисконтируя ежегодные доходы при показателе дисконта 18%. Расчеты проведем с помощью специальных таблиц.
Проект 1
|
Год |
Денежный поток |
Множитель дисконта |
Современное значение |
|
1 |
$3,000 |
0.8475 |
$2,542.50 |
|
2 |
$4,000 |
0.7182 |
$2,872.80 |
|
3 |
$5,000 |
0.6086 |
$3,043.00 |
|
4 |
$6,000 |
0.5158 |
$3,094.80 |
|
Суммарное современное значение |
$11,553.10 |
Проект 2
|
Год |
Денежный поток |
Множитель дисконта |
Современное значение |
|
1 |
$6,000 |
0.8475 |
$5,085.00 |
|
2 |
$4,000 |
0.7182 |
$2,872.80 |
|
3 |
$5,000 |
0.6086 |
$3,043.00 |
|
4 |
$3,000 |
0.5158 |
$1,547.40 |
|
Суммарное современное значение |
$12,548.20 |
По результатам расчетов можно сделать вывод о предпочтительности второго проекта.
8. Предположим Вы заключили депозитный контракт на сумму $4,000 на 3 года при 12-и процентной ставке. Если проценты начисляются ежегодно, какую сумму Вы получите по окончании контракта?
9. Финансовый менеджер предприятия предложил Вам инвестировать Ваши $10,000 в его предприятие, пообещав возвратить $13,000 через два года. Имея другие инвестиционные возможности, Вы должны выяснить, какова процентная ставка прибыльности предложенного Вам варианта.
10. Предприятие собирается приобрести через пять лет новый станок стоимостью $12,000. Какую сумму денег необходимо вложить сейчас, чтобы через пять лет иметь возможность совершить покупку, если процентная ставка прибыльности вложения составляет
а) 12 процентов?
б) 13 процентов?
11. Предприятие располагает $600,000 и предполагает вложить их в собственное производство, получая в течение трех последующих лет ежегодно $220,000. В то же время предприятие может купить на эту сумму акции соседней фирмы, приносящие 14 процентов годовых. Какой вариант Вам представляется более приемлемым, если считать что более выгодной возможностью вложения денег (чем под 14 процентов годовых) предприятие не располагает?
12. Предприятие рассматривает два альтернативных проекта капитальных вложений приводящих к одинаковому суммарному результату в отношении будущих денежных доходов:
|
Год |
Проект 1 |
Проект 2 |
|
1 |
$12,000 |
$10,000 |
|
2 |
$12,000 |
$14,000 |
|
3 |
$14,000 |
$16,000 |
|
4 |
$16,000 |
$14,000 |
|
5 |
$14,000 |
$14,000 |
|
Всего |
$ |
$ |
Оба проекта имеет одинаковый объем инвестиций. Предприятие планирует инвестировать полученные денежные доходы под 18 процентов годовых. Сравните современные значения полученных денежных доходов.
13. Вы имеете 10 млн. грн. и хотели бы удвоить эту сумму через 5 лет. Каково минимально приемлемое значение процентной ставки?
14. Банк предлагает 15% годовых. Чему должен быть равен изначальный вклад, чтобы через 3 года иметь на счете 5 млн. грн.
15. Какая сумма предпочтительнее при ставке 9% — $1000 сегодня или $2000 через 8 лет?
16. Рассчитайте наращенную сумму с исходной суммы в 2 млн. грн. при размещении ее в банке на условиях начисления сложных процентов, если годовая ставка 15%, а периоды наращения 90 дн., 180 дн., 1 год, 5 лет, 10 лет.
17. Приведены данные о денежных потоках:
|
Поток |
Год |
| |
1 |
2 |
3 |
4 |
5 |
|
А |
100 |
200 |
200 |
300 |
300 |
|
Б |
600 |
- |
- |
- |
- |
|
В |
- |
- |
- |
- |
1200 |
|
Г |
200 |
- |
200 |
- |
200 |
Рассчитайте для каждого потока показатели FV при r = 12% и PV при r = 15% для двух случаев: а) потоки имеют место в начале года; б) потоки имеют место в конце года.
18. Анализируются два варианта накопления средств по схеме аннуитета (поступление денежных средств осуществляется в конце соответствующего временного интервала):
План 1: вносится вклад на депозит $500 каждые полгода при условии, что банк начисляет 8% годовых с полугодовым начислением процентов.
План 2: делается ежегодный вклад в размере $1000 на условиях 9% годовых при ежегодном начислении процентов.
Определите:
а) какая сумма будет на счете через 10 лет при реализации каждого плана? Какой план более предпочтителен?
б) изменится ли ваш выбор, если процентная ставка в плане 2 будет снижена до 8,5%?
19. Каков ваш выбор — получение $5000 через год или $12000 через 6 лет, если коэффициент дисконтирования равен: а) 0%; б) 12%; в) 20%?
20. Рассчитайте будущую стоимость $1000 для следующих ситуаций:
а) 5 лет, 8% годовых, ежегодное начисление процентов;
б) 5 лет, 8% годовых, полугодовое начисление процентов;
в) 5 лет, 8% годовых, ежеквартальное начисление процентов.
21. Рассчитайте текущую стоимость каждого из приведенных ниже денежных поступлений, если коэффициент дисконтирования равен 12%: а) 5 млн. грн., получаемые через 3 года; б) 50 млн. грн., получаемые через 10 лет.
22. Фирме нужно накопить $2 млн., чтобы через 10 лет приобрести здание под офис. Наиболее безопасным способом накопления является приобретение безрисковых государственных ценных бумаг, генерирующих годовой доход по ставке 8% при полугодовом начислении процентов. Каким должен быть первоначальный вклад фирмы?
23. Что более предпочтительно — получить $2000 сегодня или $5000 через 8 лет, если коэффициент дисконтирования равен 8%?
24. Стоит ли покупать за $5500 ценную бумагу, генерирующую ежегодный доход в размере $1000 в течение 7 лет, если коэффициент дисконтирования равен 8%?
25. Предприятие имеет возможность участвовать в некоторой деловой операции, которая принесет доход в размере 10 млн. грн. по истечении двух лет.
- Выберите один из двух вариантов получения доходов: либо по 5 млн. грн. по истечении каждого года, либо единовременное получение всей суммы в конце двухлетнего периода.
- Существуют ли такие условия, когда выбор варианта для Вас безразличен?
- Изменится ли ваше решение, если доход второго года уменьшится до 4 млн. грн.?
Сформулируйте различные условия, при которых вариант единовременного получения дохода может быть предпочтительным.
26. Оплата по долгосрочному контракту предполагает выбор одного из двух вариантов: 25 млн. грн. через 6 лет или 50 млн. грн. через 12 лет. При каком значении коэффициента дисконтирования выбор безразличен?
27. Фирме предложено инвестировать 100 млн. грн. на срок 5 лет при условии возврата этой суммы частями (ежегодно по 20 млн. грн.); по истечении 5 лет выплачивается дополнительное вознаграждение в размере 30 млн. грн.. Примет ли она это предложение, если можно депонировать деньги в банк из расчета 8% годовых, начисляемых ежеквартально?
ПРОДОЛЖЕНИЕ >>
|
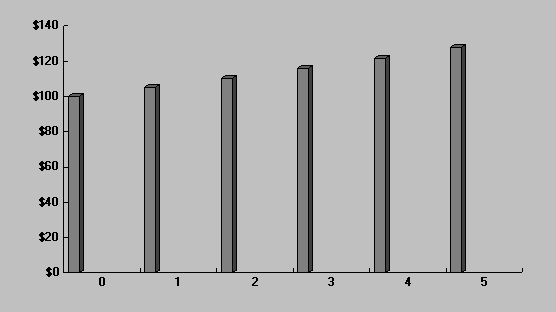

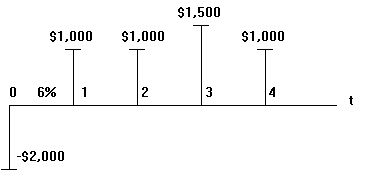
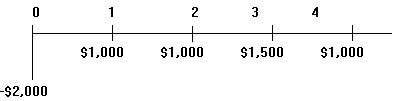
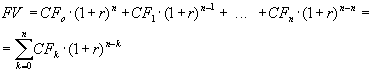 (4.5)
(4.5)